№ 22.33 Геометрія = № 45.33 Математика
На малюнку ABCD – прямокутник, M – середина відрізка AK. Доведіть, що SABCD = SAKD.
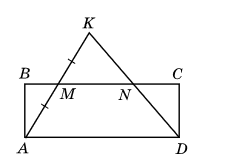
Розв'язок:
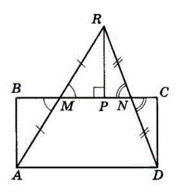
$BC || AD, M$ — середина $AK$ за умовою.
Тоді за теоремою Фалеса $N$ — середина $KD.$
Проведемо $KP ⊥ BC.$
$ΔABM = ΔKPM$ за гіпотенузою і гострим кутом ($AM = KM$ за умовою, $∠BMA = ∠KMP$ як вертикальні)
$ΔDCN = ΔKPN$ за гіпотенузою і гострим кутом ($KN = ND,$
$∠KNP = ∠DNC$ як вертикальні).
$S_{ABCD} = S_{ΔABM} + S_{AMND} +$
$+ S_{ΔDCN};$
$S_{ΔAKD} = S_{ΔMKP} + S_{AMND} + $
$+ S_{ΔKNP}.$
Оскільки $S_{ΔABM} = S_{ΔKMP},$
$S_{ΔDCN} = S_{ΔKNP},$
то $S_{ABCD} = S_{ΔAKD}.$
