№ 22.31 Геометрія = № 45.31 Математика
Одна зі сторін прямокутника на 3 см більша за іншу, а діагональ прямокутника дорівнює 15 см. Знайдіть площу прямокутника.
Розв'язок:
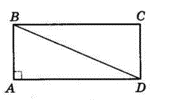
Нехай $AB = x$ см,
$AD = (x + 3)$ см, $BD = 15$ см.
З $ΔABD\ BD^2 = AB^2 + AD^2;$
$x^2 + (x + 3)^2 = 15^2;$
$x^2 + x^2 + 6x + 9 = 225;$
$2x^2 + 6x + 9 = 225;$
$2x^2 + 6x − 216 = 0; $
$x^2 + 3x − 108 = 0;$
$x_1 = −12;$
$x_2 = 9.$
Число −$12$ не задовольняє умові задачі.
Отже, $AB = 9$ см,
$AD = 9 + 3 = 12$ (см).
$S_{ABCD} = 9 · 12 = 108$ (см2).
Відповідь:
$108$ см2.
