№ 22.30 Геометрія = № 45.30 Математика
Бісектриса BK кута прямокутника ABCD поділяє сторону AD на відрізки AK = 7 см і KD = 5 см. Знайдіть площу прямокутника.
Розв'язок:
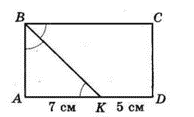
$∠BKA = ∠CBK$ як внутрішні різносторонні при паралельних прямих $AD$ і $BC$ та січній $BK.$
Але $∠KBC = ∠ABK$ за умовою.
Тоді $∠ABK = ∠BKA,$
$AB = AK = 7$ см ($ΔABK$ — рівнобедрений).
$AD = AK + KD =$
$= 7 + 5 = 12$ (см).
$SABCD = AB · AD =$
$= 7 · 12 = 84$ (см2).
Відповідь:
$84$ см2.
