№ 21.28 Геометрія = № 44.28 Математика
В опуклому п’ятикутнику ABCDE вершину B сполучено рівними між собою діагоналями з двома іншими вершинами. Відомо, що ∠BEA = ∠BDC, ∠ABE = ∠CBD. Порівняйте периметри чотирикутників ABDE і BEDC.
Розв'язок:
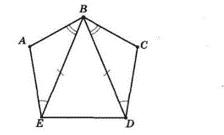
$ΔABE = ΔCBD$ за стороною і прилеглими кутами
$(BE = BD,$
$ ∠AEB = ∠CDB,$
$∠ABE = ∠CBD$ за умовою).
Тоді $AB = BC, AE = CD.$
Очевидно, що $ABDE = CBED,$ їх периметри рівні.
