ЗПЗ §§ 17–20 Геометрія = ЗПЗ §§ 36–39 Математика
Сторони трикутника дорівнюють 4 см, 13 см і 15 см. Знайдіть проекції двох менших сторін на більшу сторону.
Розв'язок:
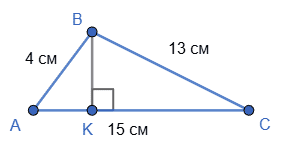
1. $BK$ − висота $△ABC.$
2. Позначимо $AK = x$ см,
тоді $KC = 15 – x$ (см).
3. У $△ABK: BK^2 = 4^2 − x^2, $
а у $△BKC:$
$ BK^2 = 13^2 − (15 − x)^2.$
4. Тоді $16 − x^2 =$
$= 169 − (225 − 30x + x^2);$
$30x = 72;$
$x = 2{,}4$ (см).
5. Отже, $AK = 2{,}4$ см;
$KC = 15 − 2{,}4 = 12{,}6$ (см).
Відповідь:
$2{,}4$ см; $12{,}6$ см.
