ВПР 3 №9 Геометрія = ВПТ 8 №9 Математика
Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 15 см, а катети відносяться як 3 : 4. Знайдіть периметр трикутника.
Розв'язок:
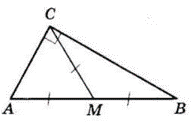
У $ΔABC (∠C = 90°) CM$ — медіана,
тоді $M$ — середина $AB,$ центр описаного кола, $AM = BM = CM = 15$ см.
Нехай $AC = 3x$ см, $BC = 4x$ см.
$AB^2 = AC^2 + BC^2;$
$(2 · 15)^2 = (3x)^2 + (4x)^2;$
$900 = 9x^2 + 16x^2;$
$25x^2 = 900;$
$x^2 = 36;$
$x = 6.$
$AC = 3 · 6 = 18$ (см);
$BC = 4 · 6 = 24$ (см).
$P_{ΔABC} = 30 + 18 + 24 = 72$ (см).
Відповідь:
$72$ см.
