ВПР 3 №8 Геометрія = ВПТ 8 №8 Математика
Більша основа рівнобічної трапеції дорівнює 26 см, висота – 12 см, а діагональ – 20 см. Знайдіть меншу основу трапеції та її бічну сторону.
Розв'язок:
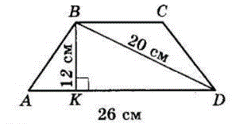
З $ΔBDK\ KD =$
$= \sqrt{BD^2 – BK^2} =$
$= \sqrt{20^2 – 12^2} =$
$= \sqrt{400 – 144} =$
$= \sqrt{256} = 16$ (см).
$AK = AD – KD =$
$= 26 – 16 = 10$ (см).
З $ΔABK\ AB =$
$= \sqrt{AK^2 + BK^2} =$
$= \sqrt{10^2 + 12^2} =$
$= \sqrt{100\ +\ 144} =$
$= \sqrt{244} = 2\sqrt{61}$ (см).
$KD\ =\ \frac{AD\ +\ BC}{2};$
$2KD = AD + BC;$
$BC = 2KD\ –\ AD =$
$= 2 · 16\ –\ 26 =$
$= 32 – 26 = 6$ (см).
Відповідь:
$6$ см, $2\sqrt{61}$ см.
