ВПР 3 №7 Геометрія = ВПТ 8 №7 Математика
Основи прямокутної трапеції дорівнюють 8 см і 17 см, а більша бічна сторона – 15 см. Знайдіть периметр трапеції.
Розв'язок:
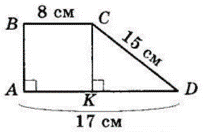
$ABCD$ – трапеція $(BC ∥ AD), BC = 8$ см, $AD = 17$ см;
$AB ⊥ AD, CD = 15$ см.
Проведемо $CK ⊥ AD,$
тоді $ABCK$ – прямокутник.
$AK = BC = 8$ см, $CK=AB.$
$KD = AD – AK = $
$= 17 – 8 = 9$ (см).
З $△CDK\ CK =$
$= \sqrt{CD^2 – KD^2} =$
$= \sqrt{15^2 – 9^2} =$
$= \sqrt{(15 – 9)(15 + 9)} =$
$= \sqrt{6 · 24} = \sqrt{6 · 6 · 4} =$
$= 6 · 2 = 12$ (см).
$P_{ABCD} = 12 + 8 + 15 + 17 =$
$= 52$ (см).
Відповідь:
$52$ см.
