ВПР 3 №33 Геометрія = ВПТ 8 №33 Математика
За двома сторонами прямокутного трикутника ABC (∠C = 90°) знайдіть його третю сторону та гострі кути:
1. $AC = 9$ см; $BC = 12$ см;
2. $AC = 7$ дм; $BC = 5$ дм;
3. $AB = 34$ см; $BC = 30$ см;
4. $AB = 8$ дм ; $AC = 7$ дм.
Розв'язок:
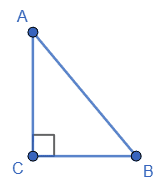
1. $AB = \sqrt{AC^2 + BC^2} =$
$= \sqrt{9^2 + 12^2} =$
$= \sqrt{81\ +\ 144\ } = $
$= \sqrt{225} = 15$ (см).
$tg\ \angle A\ =\frac{BC}{AC}=\frac{12}{9}= 1{,}333;$
$ \angle A\ \approx\ 53°8'.$
$∠B = 90° − ∠A = 36°52′.$
2. $AB = \sqrt{AC^2 + BC^2} =$
$= \sqrt{7^2 + 5^2} = $
$=\sqrt{49\ +\ 25\ } = $
$=\sqrt{74} = 8{,}6$ (дм).
$tg\ \angle A\ = \frac{BC}{AC}= \frac{5}{7}\approx\ 0{,}7143;$
$\angle A\ \approx\ 35°32'.$
$∠B = 90° − ∠A = 54°28′.$
3. $AC = \sqrt{AB^2 - BC^2} =$
$= \sqrt{34^2 - 30^2} =$
$= \sqrt{1156\ -\ 900\ } =$
$= \sqrt{256} = 16$ (см).
$sin\ \angle A\ =\ \frac{BC}{AB}=\frac{30}{34} =0{,}8824;$
$ \angle A\ \approx\ 61°56'.$
$∠B = 90° − ∠A = 28°4′.$
4. $BC = \sqrt{AB^2 - BC^2} =$
$= \sqrt{8^2 - 7^2} = $
$= \sqrt{(8\ -\ 7)(8\ +\ 7)\ } =$
$= \sqrt{15} = 3{,}87$ (дм).
$sin\ \angle B\ =\ \frac{AC}{AB}= \frac{7}{8}=0{,}875;$
$\angle B\ =\ \approx\ 61°3'.$
$∠A = 90° − ∠B = 28°57′.$
