Завдання № 31

ВПР 3 №31 Геометрія =  ВПТ 8 №31 Математика

Дано: ΔABC, ∠C = 90°. Доведіть, що sin²A + cos²A = 1. (Запис sin²A є тотожним запису (sinA)².)   

Розв'язок:

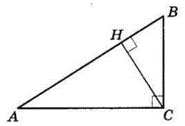
Проведемо висоту $CH$ до гіпотенузи.

З $△ABC\ AC = AB ⋅ cos ∠A,$

$ BC = AB ⋅ cos ∠B.$

З $△ACH\ cos ∠A = \frac{AH}{AC};$

$AH = AC ⋅ cos ∠A.$

Тоді $AH = (AB ⋅ cos ∠A) ⋅$

$⋅ cos ∠A = AB ⋅ cos^2 ∠A.$

З $△BCH\ BH =$

$= BC ⋅ cos ∠B =$

$= AB ⋅ cos^2 ∠B.$

$AB = AH + BH.$

$ AB = AB ⋅ cos^2 ∠A + $

$+ AB ⋅ cos^2 ∠B.$

$AB = $

$= AB (cos^2 ∠A + cos^2 ∠B);$

$cos^2 ∠A + cos^2 ∠B = 1.$

Зауважимо, що у $△ABC\ sin ∠A = \frac{BC}{AB}$ і

$cos ∠B = \frac{BC}{AB},$

тому $cos^2 ∠A + sin^2 ∠A = 1.$