ВПР 3 №30 Геометрія = ВПТ 8 №30 Математика
З точки до прямої проведено дві похилі, що утворюють з прямою кути 30° і 60°. Знайдіть відстань від точки до прямої, якщо відстань між основами похилих дорівнює a см. Скільки випадків треба розглянути?
Розв'язок:
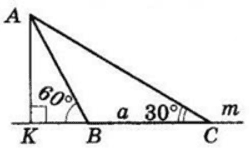
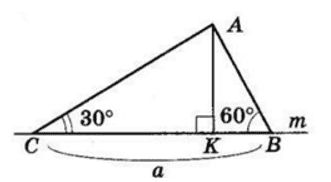
$AK ⊥ a$ — відстань від точки $A$ до прямої $m.$
а. $KB = x$ см,
$KC = (x + a)$ см.
З $△ABK\ AK = KB\ tg 60° =$
$= x\sqrt3$ (см).
З $△ACK\ AK = KC\ tg 30° =$
$= (x + a) ⋅ \frac{\sqrt3}{3}$ (см).
$x\sqrt3\ =(x\ +\ a)\ \cdot\ \frac{\sqrt3}{3};$
$x\sqrt3\ =\ \frac{x\sqrt3}{3}\ +\ \frac{a\sqrt3}{3};$
$3\sqrt3x = \sqrt3x + \sqrt3a;$
$2\sqrt3x = \sqrt3a;$
$x\ =\ \frac{a}{2}.$
Отже, $AK = \frac{\sqrt3a}{2}.$
б. $KB = x, KC = (a − x).$
З $△ACK\ AK = KC\ ⋅ tg 30° =$
$= (a - x) ⋅ \frac{\sqrt3}{3}$ (см).
З $△ABK\ AK = KB\ ⋅ tg 60° =$
$= x\sqrt3$ (см).
$x\sqrt3\ =\ (a\ -\ x)\ \cdot\ \frac{\sqrt3}{3};$
$3\sqrt3x = \sqrt3a − \sqrt3x;$
$4\sqrt3x = \sqrt3a;$
$x\ =\ \frac{\sqrt a}{4}.$
Отже, $AK = \frac{\sqrt3 a}{4}.$
Відповідь:
$\frac{\sqrt3a}{2}$ або $\frac{\sqrt3a}{4}.$
