ВПР 3 №29 Геометрія = ВПТ 8 №29 Математика
Основи трапеції дорівнюють 14 см і 10 см, кути при більшій основі дорівнюють 60° і 30°. Знайдіть висоту діагоналі трапеції.
Розв'язок:
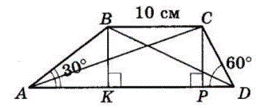
$ABCD$ — трапеція $(AD ∥ BC), AD = 14$ см, $BC = 10$ см.
$∠A = 30°, ∠D = 60°.$
Проведемо $BK ⊥ AD$ і $CP ⊥ AD$ — висоти, $BK = CP.$
$KP = BC =10$ см ($KBCP$ — прямокутник).
Тоді $AK + PD = 14 – 10 =4$ (см).
Нехай $AK = x$ см,
тоді $PD = (4 – x)$ (см).
З $△ABK\ BK = $
$= AK\ tg ∠A = x\ tg 30° = $
$= x ⋅ \frac{\sqrt3}{3}.$
З $△CPD\ CP =$
$= PD\ tg ∠D =$
$= (4 − x) tg 60° = (4 − x)\sqrt3.$
$BK\ =\ CP,\ \frac{x\sqrt3}{3}=$
$=\ (4\ -\ x)\sqrt3.$
$x\sqrt3 = 12\sqrt3 − 3\sqrt3x;$
$4\sqrt3x = 12\sqrt3;$
$x = 3.$
Отже, $AK = 3$ см, $PD = 1 $ см.
$BK = 3 ⋅ \frac{\sqrt3}{3} = \sqrt3$ (см).
З $△ACP\ AP = AK + KP = $
$=3 + 10 = 13$ см.
$AC = \sqrt{AP^2 + PC^2} =$
$= \sqrt{13^2 + (3)^2} =$
$= \sqrt{169\ +\ 3\ } =$
$= \sqrt{172} = 2\sqrt{43}$ (см).
З $△KBD\ BD =$
$= \sqrt{BK^2 + KD^2} = $
$= \sqrt{(3)^2 + (10 + 1)^2} =$
$= \sqrt{3\ +\ 121\ } = $
$= \sqrt{124} = 2\sqrt{31}$ (см).
Відповідь:
$\sqrt3$ см, $2\sqrt{43}$ см, $2\sqrt{31}$ см.
