ВПР 3 №28 Геометрія = ВПТ 8 №28 Математика
Радіус кола, вписаного в прямокутний трикутник, дорівнює r, а один із гострих кутів – β. Знайдіть катет, прилеглий до цього гострого кута.
Розв'язок:
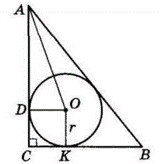
Центр кола, вписаного в трикутник, лежить в точці перетину бісектрис кутів трикутника: $AO$ — бісектриса кута $A, ∠CAO = ∠BAO = tg\frac{\beta}{2}.$
$OD ⊥ AC, OK ⊥ BC$ — радіуси кола. $CDOK$ — прямокутник, $CD = r.$
З $△AOD\ AD = \frac{OD}{tg\frac{\beta}{2}}= \frac{r}{tg\frac{\beta}{2}};$
$AC\ +\ CD\ =\ \frac{r}{tg\frac{\beta}{2}}+\ r\ =$
$= \ r(1\ +\ \frac{1}{tg\frac{\beta}{2}}).$
Відповідь:
$r(1 + \frac{1}{tg\frac{\beta}{2}}).$
