ВПР 3 №27 Геометрія = ВПТ 8 №27 Математика
У рівнобедреному трикутнику синус кута при основі дорівнює 0,96, а основа – 28 см. Знайдіть бічну сторону.
Розв'язок:
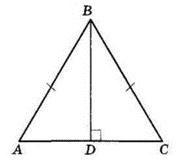
У $△ABC\ AB = BC,$
$ sin ∠A = sin ∠C = 0{,}96;$
$AC = 28$ см, $BD ⊥ AC$ — висота і медіана,
$AD = AC : 2 = 28 : 2 = 14$ (см).
$sin\ \angle A\ =\ \frac{BD}{AB}= 0{,}96\ =$
$= \frac{96}{100}\ =\ \frac{24}{25}.$
Отже, $BD : AB = 24 : 25.$
$BD = 24x$ см, $AB = 25x$ см.
З $△ABD\ AB^2 = BD^2 + AD^2;$
$(25x)^2 = (24x)^2 + 14^2;$
$625x^2 = 576x^2 + 196;$
$49x^2 = 196;$
$x^2 = 4;$
$x = 2.$
$AB = 25 ⋅ 2 = 50$ (см).
Відповідь:
$50$ см.
