ВПР 3 №23 Геометрія = ВПТ 8 №23 Математика
Катети прямокутного трикутника дорівнюють 8 см і 15 см. Знайдіть:
1. синус гострого кута, що лежить проти меншого катета;
2. косинус гострого кута, прилеглого до більшого катета;
3. тангенси обох гострих кутів.
Розв'язок:
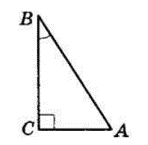
Знайдемо гіпотенузу:
$AB = \sqrt{AC^2 + BC^2} =$
$= \sqrt{8^2 + 15^2} =$
$= \sqrt{64\ +\ 225\ } = $
$= \sqrt{289} = 17$ (см).
1. $sin\ \angle B\ =\ \frac{AC}{AB}\ = \frac{8}{17};$
2. $cos\ \angle B\ =\ \frac{BC}{AB} = \frac{15}{17};$
3. $tg\ \angle A\ =\ \frac{BC}{AC}\ =\ \frac{15}{8};$
4. $tg\ \angle B\ =\ \frac{C}{BC}\ =\ \frac{8}{15}.$
