ВПР 3 №19 Геометрія = ВПТ 8 №19 Математика
3 точки до прямої проведено дві похилі, довжини яких відносяться як 13 : 15, а довжини їхніх проекцій дорівнюють 10 см і 18 см. Знайдіть довжини похилих та відстань від точки до прямої.
Розв'язок:
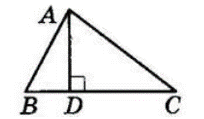
$AD ⊥ BC$ — відстань від точки $A$ до прямої $BC. AB$ і $AC$ — похилі.
$AB : AC = 13 : 15.$
$ BD = 10$ см, $CD$ = 18 см.
Нехай $AB = 13x, AC = 15x.$
З $△ABD\ AD^2 =$
$= AB^2 − BD^2 =$
$= (13x)^2 – 10^2 =$
$= 169x^2 − 100.$
З $△ACD\ AD^2 = $
$= AC^2 − CD^2 =$
$= (15x)^2 – 18^2 =$
$= 225x^2 − 324.$
$169x^2 – 100 =$
$= 225x^2 – 324;$
$225x^2 − 169x^2 =$
$= 324 − 100;$
$56x^2 = 224;$
$x^2 = 4;$
$x = 2.$
$AB = 13 ⋅ 2 = 26$ (см);
$AC = 15 ⋅ 2 = 30$ (см).
$AD = \sqrt{169 ⋅ 2^2 – 100} =$
$= \sqrt{676\ -\ 100} =$
$= \sqrt{576} = 24$ (см).
Відповідь:
$26$ см, $30$ см, $24$ см.
