ВПР 3 №18 Геометрія = ВПТ 8 №18 Математика
3 точки, що міститься на відстані 4 см від прямої, проведено до неї дві похилі. Довжина однієї з них 5 см, а друга утворює с прямою кут 45°. Знайдіть відстань між основами похилих. Скільки випадків слід розглянути?
Розв'язок:
а) 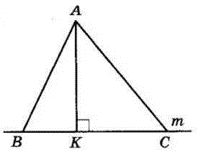
б) 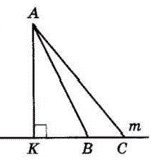
$AK ⊥ m, AK = 4$ см — відстань від точки A до прямої m.
$AB = 5$ см, $∠ACK = 45°.$
З $ΔABK\ BK =$
$= \sqrt{AB^2 – AK^2} = \sqrt{5^2 – 4^2} =$
$= \sqrt{25 – 16} = \sqrt9 = 3$ (см).
З $△ACK\ CK = AK = 4$ см ($△ACK$ — прямокутний з гострим кутом $45°$).
I випадок.
$BC = BK + KC =$
$= 3 + 4 = 7$ (см).
II випадок.
$BC = KC\ –\ BK =$
$= 4\ –\ 3 = 1$ (см).
Відповідь:
$7$ см або $1$ см.
