ВПР 3 №14 Геометрія = ВПТ 8 №14 Математика
Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 25 см. Знайдіть периметр трикутника, якщо його найменша висота дорівнює 24 см.
Розв'язок:
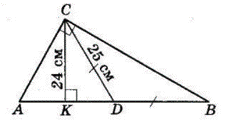
З $ΔCDK\ KD = \sqrt{CD^2 – CK^2} =$
$= \sqrt{25^2 – 24^2} =$
$= \sqrt{(25 – 24)(25 + 24)} =$
$= \sqrt{1 · 49} = 7$ (см).
$KB = KD + DB =$
$= 7 + 25 = 32$ (см) (середина гіпотенузи рівновіддалена від вершин трикутника).
З $ΔBCK\ BC =$
$= \sqrt{CK^2 + BK^2} =$
$= \sqrt{24^2 + 32^2} =$
$= \sqrt{576\ +\ 1024} =$
$= \sqrt{1600} = 40$ (см).
З $ΔABC\ AC =$
$= \sqrt{AB^2 – BC^2} =$
$= \sqrt{50^2 – 40^2} =$
$= \sqrt{(50 – 40)(50 + 40)} =$
$= \sqrt{10 · 90} = \sqrt{900} = 30$ (см).
$P_{ΔABC} = 50 + 30 + 40 =$
$= 120$ (см).
Відповідь:
$120$ см.
