ВПР 3 №13 Геометрія = ВПТ 8 №13 Математика
Бічні сторони трапеції дорівнюють 9 см і 12 см, а основи – 30 см і 15 см. Знайдіть кут, що утворюють між собою продовження бічних сторін.
Розв'язок:
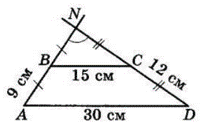
$ABCD$ — трапеція $(BC ∥ AD),$
$AB = 9$ см, $BC = 15$ см,
$CD = 12$ см, $AD = 30$ см.
$N$ — точка перетину продовжень бічних сторін.
За умовою $BC ∥ AD, BC = \frac{1}{2} AD,$
тоді $BC$ — середня лінія $△AND.$
$AN = 2AB = 2 ⋅ 9 = 18$ (см).
$DN = 2CD = 2 ⋅ 12 = 24$ (см).
$AN^2 = 18^2 = 324;$
$DN^2 = 24^2 =576;$
$AN^2 + DN^2 =$
$= 324 + 576 = 900.$
$AD2 = 302 =900.$
Отже, $AD^2 = AN^2 + DN^2.$
За теоремою, оберненою до теореми Піфагора,
у $△AND ∠N = 90°.$
Відповідь:
$90°.$
