ВПР 3 №12 Геометрія = ВПТ 8 №12 Математика
У трикутнику ABC AB = √2 см, BC = 2 см. На стороні AC позначено точку K так, що AK = KB = 1 см. Знайдіть довжину AC.
Розв'язок:
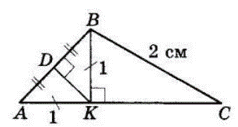
У $△ABC, AB = \sqrt2$ см, $BC = 2$ см,
$AK = KB = 1$ см.
Проведемо $KD ⊥ AB.$
У рівнобедреному $△ABK\ KD$ — висота і медіана.
$DB\ =\ \frac{1}{2}AB\ =\ \frac{\sqrt2}{2}$ (см).
$cos\ \angle DBK\ =\ \frac{DB}{BK}=$
$= \frac{\sqrt2}{2}\ ∶\ 1\ =\ \frac{\sqrt2}{2},$
звідси $∠DBK = 45°.$
$∠A = ∠DBK = 45°,$
тоді $∠AKB = 90°.$
З $△BCK\ cos ∠CBK = \frac{BK}{BC} =$
$= \frac{1}{2};$
$∠CBK = 60°.$
$∠ABC = 45° + 60° = 105°.$
Відповідь:
$105°.$
