ВПР 3 №11 Геометрія = ВПТ 8 №11 Математика
У рівнобедреному трикутнику бісектриса, проведена до бічної сторони, ділить її на відрізки 50 см і 80 см, починаючи від вершини кута між бічними сторонами. Знайдіть висоту трикутника, проведену до основи.
Розв'язок:
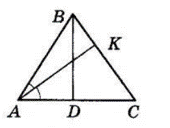
У $△ABC\ AB = BC,$
$ BD ⊥ AC, AK$ — бісектриса,
$BK = 50$ см, $KC = 80$ см.
За властивістю бісектриси кута
$\frac{AB}{AC}=\ \frac{BK}{KC}\ =\ \frac{50}{80}\ =\ \frac{5}{8},$
тобто $AB = BC = 5x$ см,
$AC = 8x$ см.
$BC = BK + KC =$
$= 50 + 80 = 130$ (см).
$5x = 130;$
$x = 26.$
$DC\ =\ \frac{1}{2}AC\ =$
$= \frac{1}{2}\ \cdot\ 8\ \cdot\ 26\ =104$ (см).
З $△BDC\ BD =$
$= \sqrt{BC^2 - CD^2} =$
$= \sqrt{130^2 - 104^2} =$
$= \sqrt{(130-104)(130+104)} =$
$= \sqrt{26\cdot\ 234} =$
$= \sqrt{26 \cdot\ 26 \cdot\ 9} = 26 ⋅ 3 = 78$ (см).
Відповідь:
$78$ см.
