ДСР 4 Геометрія = ДСР 8 Математика
Бісектриса гострого кута прямокутного трикутника ділить катет на відрізки 10 см і 26 см. Знайдіть гіпотенузу.
А. $36$ см;
Б. $38$ см;
В. $39$ см;
Г. $52$ см.
Розв'язок:
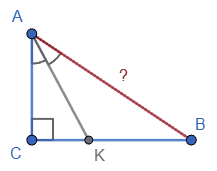
1. $AK$ — бісектриса,
тому $\frac{AC}{AB} = \frac{CK}{KB}.$
2. Оскільки $AC < AB$,
то $CK < KB.$
$ CK = 10$ см; $KB = 26$ см.
3. Маємо $\frac{AC}{AB} =\frac{10}{26} = \frac{5}{13}.$
Можна позначити $AC = 5x$ см; $AB = 13x$ см.
4. $AB^2 = AC^2 + CB^2;$
$(13x)^2 = (5x)^2 + 36^2;$
$144x^2 = 36^2;$
$x^2 = 9;$
$x = 3$ (см).
5. $AB = 13 ⋅ 3 = 39$ (см).
Відповідь:
В. $39$ см.
