№ 20.5 Геометрія = № 39.5 Математика
Діагональ прямокутника дорівнює 6 см й утворює кут 25° з однією з його сторін. Знайдіть кут, що утворює діагональ прямокутника з другою стороною, та сторони прямокутника (з точністю до сотих см).
Розв'язок:
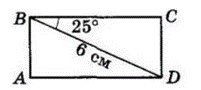
З $ΔBCD\ ∠BDC =$
$= 90° – ∠CBD =$
$= 90° – 25° = 65°.$
$BC = BD\ cos ∠CBD =$
$= 6\ cos 25° ≈ 6 · 0{,}9063 ≈ $
$≈5{,}44$ (см).
$CD = BD\ sin ∠CBD =$
$= 6\ sin 25° ≈$
$ ≈ 6 · 0{,}4226 ≈ 2{,}54$ (см).
Відповідь:
$65°, 5{,}44$ см, $2{,}54$ см.
