№ 20.4 Геометрія = № 39.4 Математика
За катетом трикутника ABC (∠C = 90°) і його гострим кутом знайдіть інші сторони та другий гострий кут трикутника (сторони трикутника в задачах 2 і 3) знайдіть із точністю до сотих.
1. AC = 10 см; ∠A = 60°;
2. AC = 8 дм; ∠B = 12°;
3. BC = 6 см; ∠B = 71°;
4. BC = 12 дм; ∠A = 45°.
Розв'язок:
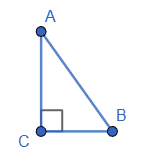
1. ∠B = 90° − ∠A =
= 90° − 60° = 30°.
AB = 2AC = 2 · 10 = 20 (см).
BC = AC tg ∠A = 10 tg 60° ≈
≈ 10 · 1,732 ≈ 17,32 (см).
2. ∠A = 90° − ∠B =
= 90° − 12° = 78°.
$BC = \frac{AC}{tg\ \angle B} = 8tg 12° ≈ $
$≈ \frac{8}{0,2126} ≈ 37,63$ (дм).
$AB = \frac{AC}{sin\ \angle B} = 8sin 12° ≈ $
$≈ \frac{8}{0,2079} ≈ 38,48$ (дм).
3. ∠A = 90° − ∠B =
= 90° − 71° = 19°.
AC = BC tg ∠B = 6 · tg 71° ≈
≈ 6 · 2,904 ≈ 17,42 (см).
$AB = BC : cos ∠B = $
$ = BCcos 71° ≈ \frac{6}{0,3256} ≈ 18,43$ (см).
4. ∠B = 90° − ∠A =
= 90° − 45° = 45°.
AC = BC = 12 дм.
$AB = \frac{BC}{sin\ \angle A} = $
$= 12 : \frac{\sqrt2}{2} = 12\sqrt2$ (дм).
Відповідь:
1. 30°, 20 см, 17,32 см.
2. 78°, 37,63 дм, 38,48 дм.
3. 19°, 17,42 см, 18,43 см.
4. 45°, 12 дм, $12\sqrt2$ дм.
