№ 20.21 Геометрія = № 39.21 Математика
Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки, які дорівнюють 30 см і 40 см. Знайдіть найменшу сторону трикутника.
Розв'язок:
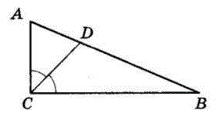
За властивістю бісектриси кута трикутника
$AC∶ CB = \frac{AD}{DB} = \frac{30}{40} = \frac{3}{4}.$
Нехай $AC = 3x$ см,
а $CB = 4x$ см.
За теоремою Піфагора
$AB^2 = AC^2 + BC^2;$
$(30 + 40)^2 = (3x)^2 + (4x)^2; $
$4900 = 9x^2 + 16x^2;$
$4900 = 25x^2;$
$x^2 = 196; $
$x = 14.$
$AC = 3 · 14 = 42$ (см).
Відповідь:
$42$ см.
