№ 20.20 Геометрія = № 39.20 Математика
У ∆ABC ∠C = 90°, BC = 12 см, sin B = $\frac{3}{5}.$ Знайдіть периметр трикутника.
Розв'язок:
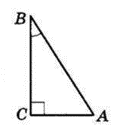
$sin ∠B = \frac{AC}{AB} = \frac{3}{5}.$
Нехай $AC = 3x, AB = 5x.$
Тоді за теоремою Піфагора
$AB^2 = AC^2 + BC^2;$
$(5x)^2 = (3x)^2 + 12^2; $
$25x^2 = 9x^2 + 144; $
$16x^2 = 144; $
$x^2 = 9; $
$x = 3.$
Отже, $AC = 3 · 3 = 9$ (см),
$AB = 5 · 3 = 15$ (см).
$P_{∆ABC} = 12 + 9 + 15 = 36$ (см).
Відповідь:
$36$ см.
