№ 20.19 Геометрія = № 39.19 Математика
Діагоналі ромба дорівнюють 16 см і 30 см. Знайдіть периметр ромба.
Розв'язок:
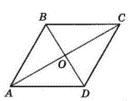
$BD = 16$ см, $AC = 30$ см.
$BD ⊥ AC,$
$BO=\frac{1}{2}BD=\frac{1}{2}·16=8$ см;
$AO=\frac{1}{2}AC=\frac{1}{2}·30=15$ (см) (властивості діагоналей ромба).
З $∆AOB\ AB = \sqrt{AO^2 + BO^2} =$
$= \sqrt{15^2 + 8^2} =$
$= \sqrt{225\ +\ 64\ } = \sqrt{289} = 17$ (см).
Відповідь:
$17$ см.
