№ 20.18 Геометрія = № 39.18 Математика
На горі розміщена башта, висота якої l м. За деяким об’єктом A, що розміщений бiля пiднiжжя гори, спостерігають спочатку з вершиною M башти під кутом 60° до горизонту, а потім вiд основи башти N пiд кутом 30°. Знайдіть висоту x гори.
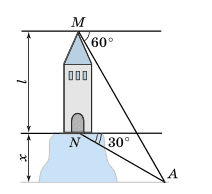
Розв'язок:
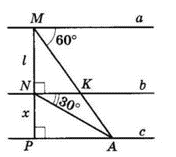
$a ∥ b ∥ c.$
Тоді $∠MAP = 60°$ (внутрішні різносторонні).
$∠KNA = ∠NAP = 30°$ (внутрішні різносторонні);
$∠NAK = ∠KAP – ∠NAP = $
$= 60° – 30° = 30°.$
Тоді $∆NKA$ – рівнобедрений, $ NK = KA. $
З $∆MNK: ∠NMK =$
$= 90° – 60° = 30°.$
$MN\ =\ l,$
$ NK\ =\ MN\ tg\ 30° = \frac{l\sqrt3}{2};$
$MK\ = \frac{MN}{cos 30°} = \frac{2l}{\sqrt3} = \frac{2\sqrt3l}{3}.$
Тоді $AK = \frac{2\sqrt3l}{3};$
$AM\ =\ MK\ +\ AK\ =$
$= \frac{\sqrt3l}{3}\ +\ \frac{2\sqrt3l}{3}\ =\ \frac{3\sqrt3l}{3}\ =$
$= \sqrt{3l}.$
З $∆AMP\ MP= AM\ cos 30° =$
$= 3 · l · \frac{\sqrt3}{2} = \frac{3}{2}l.$
$NP\ =\ MP\ – MN = \frac{3}{2} l – l =$
$= \frac{1}{2} l.$
Відповідь:
$\frac{1}{2} l.$
