№ 19.40 Геометрія = № 38.40 Математика
У трикутнику одна зі сторін дорівнює 10 см, а прилеглі до неї кути –
135° і 30°. Знайдіть висоту трикутника, проведену до даної сторони.
Розв'язок:
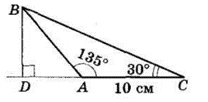
Тоді $ΔABD$ — рівнобедрений: $BD = AD.$
Нехай $AD = x$ см,
тоді $CD = (x + 10)$ см.
З $ΔBCD\ BD = CD · tg ∠C =$
$= (x + 10) · tg\ 30° =$
$= 33(x + 10)$ (см).
З $ΔABD\ BD = AD · tg ∠A =$
$= x\ tg\ 45° = x$ (см).
$\frac{\sqrt3}{3}(x\ +\ 10)\ =\ x;$
$\frac{\sqrt3}{3}x\ +\ \frac{10\sqrt3}{3}\ =\ x;$
$(1\ -\ \frac{\sqrt3}{3})x\ = \frac{10\sqrt3}{3};$
$\frac{(3\ -\ \sqrt3)x}{3}=\ \frac{10\sqrt3}{3};$
$(3 − \sqrt3)x = 10\sqrt3;$
$x\ =\ \frac{10\sqrt3}{3\ -\ \sqrt3}\ =\ \frac{10\sqrt3}{\sqrt3\ (\sqrt3\ -\ 1)}\ =$
$= \ \frac{10(\sqrt3\ +\ 1)}{(\sqrt3\ -\ 1)(\sqrt3\ +\ 1)}\ =$
$= \ \frac{10(\sqrt3\ +\ 1)}{3\ -\ 1}\ =\ 5(\sqrt3\ +\ 1)$ (см).
Відповідь:
$5(\sqrt3 + 1) см.$
