№ 19.38 Геометрія = № 38.38 Математика
Гострий кут паралелограма дорівнює 45°. Діагональ ділить тупий кут у відношенні 1 : 2. Знайдіть цю діагональ, якщо периметр паралелограма дорівнює 20 см.
Розв'язок:
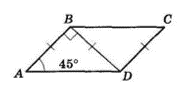
$ABCD$ — паралелограм.
$∠A = ∠C = 45°. $
$∠CBD : ∠ABD = 1 : 2.$
$∠ABC = 180° − ∠A =$
$= 180° − 45° = 135°.$
Позначимо $∠CBD = x, ∠ABD = 2x.$
$x + 2x = 135°; $
$3x = 135°; $
$x = 45°.$
Отже, $∠CBD = 45°,$
$ ∠ABD = 45° \cdot 2 = 90°.$
У $ΔABD\ ∠BDA = ∠BAD =$
$= 45°,$
тоді $AB = BD;$
$AD\ = \frac{AB}{cos 45°} = AB∶ \frac{1}{\sqrt2} =$
$= \sqrt2AB.$
$P_{ABCD} = 2(AB + AD) =$
$= 2(AB + \sqrt2AB) =$
$= 2AB(1 + \sqrt2).$
За умовою $2AB(1 + \sqrt2) = 20;$
$2AB(1 + \sqrt2) = 20;$
$AB(1 + \sqrt2) = 10;$
$AB\ =\ \frac{10}{1\ +\ \sqrt2}=$
$= \frac{10(\sqrt2 – 1)}{(1\ +\ \sqrt2)(\sqrt2 - 1)} = \frac{10(\sqrt2 – 1)}{(\sqrt2)^2 - 1} = $
$= 10(\sqrt2 – 1)$ (см).
$BD = AB = 10(\sqrt2 − 1)$ (см).
Відповідь:
$10(\sqrt2 − 1)$ см.
