№ 19.36 Геометрія = № 38.36 Математика
Бічна сторона рівнобедреного трикутника дорівнює m, а кут при основі – α. Знайдіть радіус кола, вписаного в цей трикутник.
Розв'язок:
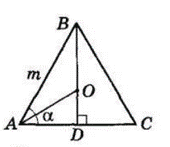
Центр $O$ кола, вписаного в $ΔABC,$ лежить у точці перетину бісектрис кутів.
$AO$ — бісектриса кута $A, BD$ — бісектриса, висота і медіана, проведена з вершини $B.$
З $ΔABD\ AD = AB\ cos α =$
$= m\ cos α.$
З $ΔAOD ∠OAD = \frac{\alpha}{2}, OD$ — радіус вписаного кола.
$OD = AD · tg ∠OAD = $
$= m\ cos α · tg \frac{\alpha}{2}.$
Відповідь:
$m\ cos α · tg \frac{\alpha}{2}.$
