№ 19.35 Геометрія = № 38.35 Математика
Діагоналі ромба дорівнюють 10 см і 12 см. Знайдіть кути ромба (з точністю до хвилини).
Розв'язок:
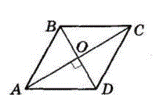
$ABCD$ — ромб, $AC = 12$ см,
$BD = 10$ см.
$AO\ =\ \frac{1}{2}AC\ =\ \frac{1}{2}\ \cdot\ 12\ =$
$= \ 6$ (см);
$BO\ =\ \frac{1}{2}BD\ =\ \frac{1}{2}\ \cdot\ 10\ =$
$= \ 5$ (см).
У $ΔAOB ∠O = 90°$ (за властивістю діагоналей).
$\angle BAO\ =\ \frac{1}{2}\angle A.$
$tg\ \angle BAO\ =\ \frac{BO}{AO}\ =$
$= \ \frac{5}{6}\ \approx\ 0{,}8333.$
$∠BAO ≈ = 39°48'.$
$∠A = 2∠BAO = 2 \cdot 39°48' =$
$= 79°36'.$
$∠C = ∠A = 79°36'.$
$∠B = ∠D = 180° − 79°36' =$
$= 100°24'.$
Відповідь:
$79°36', 100°24'.$
