№ 19.33 Геометрія = № 38.33 Математика
На малюнку ∠ACB = ∠K = 90°, BK = a, ∠ABC = β, ∠BCK = α. Знайдіть BC, AC, AB.
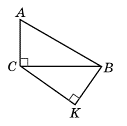
Розв'язок:
З $ΔBCK\ BC = \frac{BK}{sin\ \alpha} = \frac{a}{sin\ \alpha}.$
З $ΔABC\ AC = BC\ tg\ β =$
$= \frac{a\ tg\ \beta}{sin\ \alpha};$
$AB\ =\ \frac{BC}{cos\ \beta}\ =\ \frac{a}{sin\ \alpha\ cos\ \beta}.$
Відповідь:
$\frac{a}{sin\ \alpha}, \frac{a\ tg\ \beta}{sin\ \alpha}, \frac{a}{sin\ \alpha\ cos\ \beta}.$
