№ 19.29 Геометрія = № 38.29 Математика
Дано: ΔABC, ∠C = 90°. Знайдіть:
а. AB і BC, якщо AC = 6 см,
cos B = 0,8;
б. AC і BC, якщо AB = 13 см,
tg A = $\frac{5}{12}.$
Розв'язок:
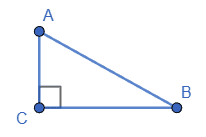
а) За умовою $cos ∠B = 0{,}8 = \frac{4}{5},$
тобто $\frac{BC}{AB} = \frac{4}{5}.$
Позначимо $BC = 4x, AB = 5x. $
За теоремою Піфагора: $AB^2 = AC^2 + BC^2;$
$(5x)^2 = 6^2 + (4x)^2;$
$25x^2 = 36 + 16x^2;$
$25x^2 − 16x^2 = 36;$
$9x^2 = 36; $
$x^2 = 4;$
$x = 2. $
Отже, $BC = 4 · 2 = 8$ (см),
$AB = 5 · 2 = 10$ (см).
б) За умовою $tg ∠A = \frac{5}{12},$
тобто $\frac{BC}{AC} = \frac{5}{12}.$
Позначимо $BC = 5x, AB = 12x.$
За теоремою Піфагора: $AB^2 = AC^2 + BC^2;$
$13^2 = (12x)^2 + (5x)^2;$
$169 = 144x^2 + 25x^2;$
$169x^2 = 169;$
$x^2 = 1;$
$x = 1.$
$BC = 5 · 1 = 5$ (см),
$AC = 12 · 1 = 12$ (см).
Відповідь:
а) 8 см, 10 см;
б) 5 см, 12 см.
