№ 19.24 Геометрія = № 38.24 Математика
Сторона ромба дорівнює 8 см, а один з його кутів – 78°. Знайдіть (з точністю до сотих сантиметра) діагональ ромба, що виходить із цього кута.
Розв'язок:
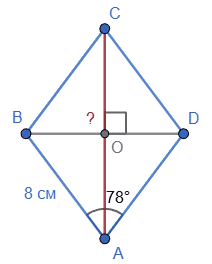
В ромб $ABCD ∠A = 78°, $
$AB = BC = CD = AD = 8$ см.
За властивістю діагоналей ромба $AC ⊥ BD, $
$\angle BAO\ =\ \angle DAO\ =$
$=\ 78°∶ 2 = 39°,$
$AO = \frac{1}{2}AC.$
З $ΔAOB\ cos ∠BAO =$
$= AO : AB;$
$AO = AB · cos ∠BAO = $
$= 8 · cos 39° ≈ 8 · 0{,}7771 ≈$
$ ≈ 6{,}22$ (см).
$AC = 2 · 6{,}22 = 12{,}44$ (см).
Відповідь:
$12,44$ см.
