№ 19.23 Геометрія = № 38.23 Математика
Кут ромба дорівнює 42°, а діагональ, що лежить проти нього, – 6 см. Знайдіть другу діагональ ромба (з точністю до сотих сантиметра).
Розв'язок:
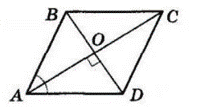
У ромбі $ABCD\ ∠A = 42°; BD = 6$ см.
За властивістю діагоналей ромба $AC ⊥ BD,$
$∠BAO = ∠DAO = 42° : 2 =$
$= 21°,$
$BO\ =\ \frac{1}{2}BD\ =\ \frac{1}{2}\ · 6 =$
$= 3$ (см).
З $ΔAOB\ AO = \frac{BO}{tg ∠BAO} =$
$= \frac{3}{tg 21°} ≈ \frac{3}{0,3839} ≈$
$≈ 7{,}8145$ (см).
$AC = 2AO = 2 · 7{,}8145 =$
$= 15{,}63$ (см).
Відповідь:
$15{,}63$ см.
