№ 18.26 Геометрія = № 37.26 Математика
У △ ABC (∠C = 90°) проведено середню лінію KL. KL = 3 см, LB = 4 см.
1. У ΔKBL та ΔABC знайдіть відношення катета, протилежного до кута B, до катета, прилеглого до кута B, і порівняйте отримані значення.
2. У ΔKBL та ΔABC знайдіть відношення катета, протилежного до кута B, до гіпотенузи та порівняйте отримані значення.
3. У ΔKBL і ΔABC знайдіть відношення катета, прилеглого до кута B, до гіпотенузи та порівняйте отримані значення.
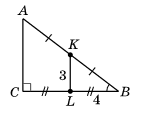
Розв'язок:
1. У $ΔKBL\ \frac{KL}{BL} = \frac{3}{4};$
у $ΔABC \frac{AC}{BC} = \frac{2 · 3}{2 · 4} = \frac{3}{4}.$
Отже, $\frac{KL}{BL} = \frac{AC}{BC}.$
2. У $ΔKBL\ BK = $
$= \sqrt{KL^2 + LB^2} = $
$\sqrt{3^2 + 4^2} = \sqrt{9\ +\ 6} =$
$ = \sqrt{25} = 5.$
$\frac{KL}{KB}\ =\ \frac{3}{5}.$
У $ΔABC\ AB = 2KB =$
$= 2 · 5 = 10$ см;
$AC = 2KL = 2 · 3 = 6.$
$\frac{AC}{AB}\ =\ \frac{6}{10}\ =\ \frac{3}{5}.$
$ \frac{KL}{KB}\ =\ \frac{AC}{AB}.$
3. У $ΔKBL\ \frac{BL}{KB} = \frac{4}{5};$
у $ΔABC\ \frac{BC}{AB} = \frac{8}{10} = \frac{4}{5}.$
$\frac{BL}{KB}=\ \frac{BC}{AB}.$
