№ 18.25 Геометрія = № 37.25 Математика
Радіуси двох кіл, які мають зовнішній дотик, дорівнюють 1 см і 4 см. Пряма a – спільна дотична цих кіл. Знайдіть відстань між точками дотику прямої a з колами.
Розв'язок:
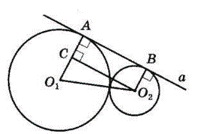
$O_1A ⊥ a, O_2B ⊥ a$ — радіуси, проведені в точці дотику.
$O_1O_2$ — відрізок, що з'єднує центри кіл.
Проведемо $O_1C ⊥ O_2A.$
$CABO_2$ — прямокутник
$(AB || CO_2, AC || BO_2,$
$ AC ⊥ AB),$
тоді $CO_2 = AB, O_2B = CA,$
тому $O_1C = O_1A – AC =$
$= 4 – 1 = 3$ (см).
З $ΔO_1CO_2 (∠C = 90°)$
$CO_2 = \sqrt{O_2O_2^2 – CO_1^2} =$
$=\sqrt{(1 + 4)^2 – 3^2} =$
$= \sqrt{25 – 9} = \sqrt{16} = 4$ (см).
Відповідь:
$4$ см.
