№ 18.24 Геометрія = № 37.24 Математика
3 точки A до прямої m проведено похилі AB і AC та Основи рівнобічної трапеції дорівнюють 5 см і 11 см, а її висота – 6 см. Знайдіть діагональ трапеції.
Розв'язок:
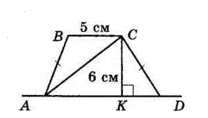
$ABCD$ — трапеція,
$AB = CD, CK = 6$ см,
$CK ⊥ AD.$
$BC = 5$ см, $AD = 11$ см.
$AK\ =\ \frac{BC\ +\ AD}{2};$
$AK\ =\ \frac{5\ +\ 11}{2}=\ \frac{16}{2}\ =\ 8$ (см).
З $ΔACK (∠K = 90°)$
$AC = AK^2 + CK^2 = $
$= 8^2 + 6^2 = \sqrt{64\ +\ 36} = $
$= \sqrt{100} = 10$ (см).
Відповідь:
10 см.
