№ 18.23 Геометрія = № 37.23 Математика
3 точки A до прямої m проведено похилі AB і AC та перпендикуляр AK, причому точка K лежить між точками B і C. AB = 15 см, AK = 12 см, KC = 16 см. Знайдіть ∠ BAC.
Розв'язок:
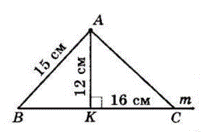
$AB$ і $AM$ — похилі до прямої $m, AB = 15$ см.
$AK ⊥ m, AK = 12$ см,
$KC = 16$ см.
З $ΔABK\ BK =$
$= \sqrt{AB^2 - AK^2} = $
$= \sqrt{15^2 - 12^2} =$
$= \sqrt{225\ -\ 144} = \sqrt{81} = 9$ (см).
З $ΔAKC\ AC =$
$= \sqrt{AK^2 + KC^2} =$
$= \sqrt{12^2 + 16^2} = $
$=\sqrt{144\ +\ 256} = $
$= \sqrt{400} = 20$ (см).
$BC = BK + KC =$
$= 9 + 16 = 25$ (см).
У $ΔABC\ AB^2 = 15^2 = 225;$
$AC^2 = 20^2 = 400;$
$BC^2 = 25^2 = 625.$
$625 = 225 + 400.$
Отже, $BC^2 = AB^2 + AC^2.$
Тоді за оберненою теоремою Піфагора $∠A = 90°.$
Відповідь:
90°.
