№ 18.22 Геометрія = № 37.22 Математика
Сторони гострокутного трикутника дорівнюють 25 см, 29 см і 36 см. Знайдіть проєкції двох більших сторін на меншу сторону.
Розв'язок:
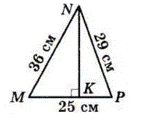
У $ΔMNP\ MN = 36$ см,
$NP = 29$ см, $MP = 25$ см.
Проведемо $NK ⊥ MP$ — перпендикуляр, проведений з вершини $N$ до меншої сторони $MP.$
$MK$ — проекція сторони $MN, KP$ — проекція сторони $NP$ на сторону $MP.$
Нехай $MK = x$ см,
тоді $PK = (25 − x)$ см.
З $ΔMNK\ NK^2 = $
$= MN^2 − MK^2 = 36^2 − x^2 =$
$= 1296 − x^2.$
З $ΔNPK\ NK^2 =$
$= NP^2 − PK^2 =$
$= 29^2 − (25 − x)^2 =$
$= 841 − 625 + 50x − x^2 =$
$= 50x − x^2 + 216.$
Ліві частини рівності однакові, тоді і праві частини рівні.
$1296 − x^2 =50x − x^2 + 216;$
$50x = 1296 − 216;$
$50x = 1080;$
$x = 21{,}6.$
Отже, $MK = 21{,}6$ см,
$PK = 25 − 21{,}6 = 3{,}4$ (см).
Відповідь:
$21{,}6$ см, $3{,}4$ см.
