№ 18.21 Геометрія = № 37.21 Математика
Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть проєкції двох менших сторін на більшу сторону.
Розв'язок:
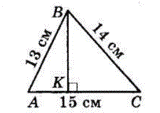
У $ΔABC\ AB = 13$ см, $BC = 14$ см,
$AC = 15$ см.
Проведемо $BK ⊥ AC$ — перпендикуляр, проведений з вершини $B$ до більшої сторони $AC.$
$AK$ — проекція сторони $AB, CK$ — проекція сторони $CB$ на сторону $AC.$
Нехай $AK = x$ см,
тоді $CK = (15 − x)$ см.
З $ΔABK\ BK^2 =$
$= AB^2 − AK^2 = 13^2 − x^2 =$
$= 169 − x^2.$
З $ΔBCK\ BK^2 =$
$= BC^2 − CK^2 =$
$= 14^2 − (15 − x)^2 =$
$= 196 − 225 + 30x − x^2 =$
$= −29 + 30x − x^2.$
Ліві частини рівності однакові, тоді і праві частини рівні.
$169 − x^2 = −29 + 30x − x^2;$
$30x = 198;$
$x = 6{,}6.$
Отже, $AK = 6{,}6$ см,
$CK = 15 − 6{,}6 = 8{,}4$ (см).
Відповідь:
$6,6$ см, $8,4$ см.
