№ 18.19 Геометрія = № 37.19 Математика
3 точки до прямої проведено дві похилі завдовжки 10 см і 14 см, різниця проєкцій яких дорівнює 8 см. Знайдіть проєкції похилих та відстань від точки до прямої.
Розв'язок:
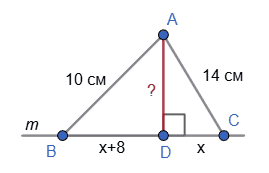
$AB = 10$ см, $AC = 14$ см — похилі,
$AD ⊥ BC$ — відстань від точки $A$ до прямої $BC.$
$BD$ — проекція $AB, CD$ — проекція $AC.$
$AB < AC,$ тому $BD < CD.$
Нехай $BD = x$ см,
тоді $CD = (x + 8)$ см.
З $ΔABD\ AD^2 =$
$= AB^2 − BD^2 = 10^2 − x^2 =$
$= 100 − x^2.$
З $ΔACD\ AD^2 =$
$= AC^2 − CD^2 =$
$= 14^2 − (x + 8)^2 =$
$= 196 − x^2 − 16x − 64 =$
$= 132 − x^2 − 16x.$
Звідси $100 − x^2 = 132 − x2 − 16x;$
$16x = 32;$
$x = 2.$
$BD = 2$ см,
$CD = 2 + 8 = 10$ (см).
$AD = \sqrt{100 - 2^2} = $
$= \sqrt{100\ -\ 4} = \sqrt{96} =$
$= \sqrt{16 · 6} = 4\sqrt6$ (см).
Відповідь:
$2$ см, $10$ см, $4\sqrt6$ см.
