№ 18.17 Геометрія = № 37.17 Математика
Точки M і N лежать по один бік від прямої a. Із цих точок до прямої a проведено перпендикуляри завдовжки 2 см і 7 см. Знайдіть відстань між основами перпендикулярів, якщо MN = 13 см.
Розв'язок:
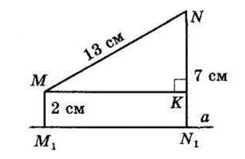
$MM_1 ⊥ a, NN_1 ⊥ a, $
$MM_1 = 2$ см, $NN_1 = 7$ см,
$MN = 13$ см.
Проведемо $MK ⊥ NN_1.$
$M_1MKN_1$ — прямокутник
$(MM_1 || KN_1, MK || M_1N_1,$
$∠MKN_1 = 90°). $
$M_1N_1 = MK, $
$KN_1 = MM_1 = 2$ см.
З $ΔMKN\ NK = $
$= NN_1 − KN_1 =$
$= 7 см − 2 см = 5$ см.
$MK = \sqrt{MN^2 - NK^2} =$
$= \sqrt{13^2 - 5^2} = \sqrt{169\ -\ 25} =$
$= \sqrt{144} = 12$ (см).
$M_1N_1 = MK = 12$ см.
Відповідь:
$12$ см.
