№ 18.16 Геометрія = № 37.16 Математика
З точки до прямої проведено дві похилі. Довжина однієї з похилих дорівнює 41 см, а її проекція – 9 см. Який кут утворює інша похила з прямою, якщо її проєкція на пряму дорівнює 40 см?
Розв'язок:
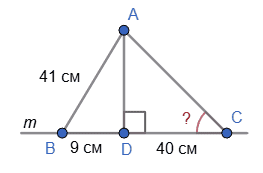
$AB = 41$ см і $AC$ — похилі,
$AD ⊥ BC.$
$BD = 9$ см, $CD = 40$ см — проекції похилих.
З $ΔABD\ AD =$
$= \sqrt{AB^2 - BD^2} =$
$= \sqrt{41^2 - 9^2} =$
$= \sqrt{(41\ -\ 9)(41\ +\ 9)} =$
$= \sqrt{32 · 50} =$
$= \sqrt{16 · 2 · 2 · 25} =$
$= 4 · 2 · 5 = 40$ (см).
У $ΔACD\ AC = CD,$
тоді $ΔACD$ — прямокутний і рівнобедрений,
$∠ACD = 45°.$
Відповідь:
$45°.$
