№ 18.13 Геометрія = № 37.13 Математика
З точки, що міститься на відстані 24 см від прямої, проведено дві похилі завдовжки 25 см і 26 см. Знайдіть відстань між основами похилих. Скільки випадків слід розглянути?
Розв'язок:
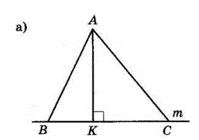
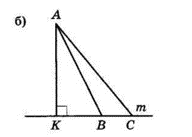
$AK ⊥ m$ — перпендикуляр, $AK = 24$ см.
$AB = 25$ см і $AC = 26$ см — похилі.
З $ΔABK\ BK =$
$= \sqrt{AB^2 - AK^2} =$
$= \sqrt{25^2 - 24^2} =$
$= \sqrt{(25\ -\ 24)(25\ +\ 24)} =$
$= \sqrt{1 · 49} = 7$ (см).
З $ΔACK\ KC =$
$= \sqrt{AC^2 - AK^2} =$
$= \sqrt{26^2 - 24^2} =$
$= \sqrt{(26\ -\ 24)(26\ +\ 24)} =$
$= \sqrt{2 · 50} = \sqrt{100} = 10$ (см).
I випадок. Точки $B$ і $C$ лежать по різні сторони від $K.$
$BC = BK + KC =$
$= 7 + 10 = 17$ (см).
II випадок. Точки $B$ і $C$ лежать по один бік від $K.$
$BC = CK − BK = $
$=10 − 7 = 3$ (см).
Відповідь:
$17$ см або $3$ см.
