№ 18.11 Геометрія = № 37.11 Математика
З точки до прямої проведено дві похилі. Одна з них дорівнює 12 см та утворює з прямою кут 30°. Знайдіть довжину другої похилої, якщо її проєкція на пряму – 8 см.
Розв'язок:
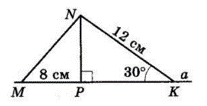
$NM$ і $NK$ — похилі,
$NK = 12$ см. $NP ⊥ a.$
$MP = 8$ см — проєкція похилої
$NM, ∠NKP = 30°.$
З $ΔNKP\ NP = \frac{1}{2}NK =$
$= \frac{1}{2} · 12 см = 6$ см
(за властивістю катета, що лежить проти кута $30°$).
З $ΔNMP\ MN =$
$= \sqrt{NP^2 + MP^2} =$
$= \sqrt{8^2 + 6^2} = \sqrt{64\ +\ 36} =$
$= \sqrt{100} = 10$ (см).
Відповідь:
$10$ см.
