№ 18.10 Геометрія = № 37.10 Математика
З точки до прямої проведено дві похилі. Одна з них дорівнює 13 см, а її проекція – 5 см. Знайдіть проекцію другої похилої, якщо вона утворює з прямою кут 45°.
Розв'язок:
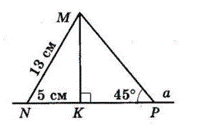
$MN$ і $MP$ — похилі, проведені з точки $M$ до прямої a, $MN = 13$ см.
Проведемо $MK ⊥ a$ — перпендикуляр.
$NK = 5$ см — проєкція похилої $NK, KP$ — проєкція похилої $MP, ∠MPK = 45°.$
З $ΔMNK\ MK =$
$= \sqrt{MN^2 - NK^2} =$
$= \sqrt{13^2 - 5^2} =$
$= \sqrt{169\ -\ 25} = \sqrt{144} = 12$ (см).
У $ΔMPK ∠PMK =$
$= 90° − 45° = 45°.$
Тоді $ΔMPK$ — рівнобедрений,
$MK = KP = 12$ см.
Відповідь:
$12$ см.
