№ 17.53 Геометрія = № 36.53 Математика
Коло радіуса 3 см вписано в ромб. Один з відрізків, на які точка дотику ділить сторону ромба, дорівнює 9 см. Знайдіть периметр ромба.
Розв'язок:
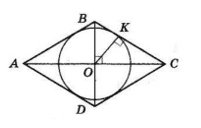
$ABCD$ — ромб, $O$ — точка перетину його діагоналей і центр вписаного кола.
$OK ⊥ BC$ — радіус, проведений в точку дотику.
$OK = 3$ см, $KC = 9$ см.
З $ΔOKC OC^2 = $
$= OK^2 + KC^2 = 3^2 + 9^2 =$
$= 9 + 81 = 90.$
З $ΔBOC\ OC^2 = BC ⋅ KC,$
$BC = OC^2 : KC =$
$= 90 : 9 = 10$ (см).
$P_{ΔABC} = 4 ⋅ BC = $
$= 4 ⋅ 10 = 40$ (см).
Відповідь:
$40$ см.
