№ 17.54 Геометрія = № 36.54 Математика
Трапецію вписано в коло так, що діаметр кола є її більшою основою, а відношення основ дорівнює 2 : 1. Знайдіть кути трапеції.
Розв'язок:
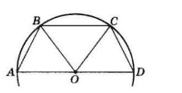
$ABCD$ — трапеція, вписана в півколо.
$AD$ — діаметр кола.
Проведемо $BO$ і $CO$ — радіуси кола.
Тоді $AO = BO = $
$= CO = DO = BC$ як радіуси кола,
$BC\ =\ \frac{1}{2}AD$ за умовою,
$ΔBOC$ — рівносторонній, всі його кути дорівнюють $60°.$
$∠BOA = ∠COD$ як внутрішні різносторонні з кутами $CBO$ і $BCO$ відповідно.
Тоді в рівнобедрених трикутниках $ABO$ і $DOC$ решта кутів також дорівнюють $60°.$
Отже, у трапеції $ABCD ∠A = ∠D = 60°,$
$∠B = ∠C = 120°.$
Відповідь:
$60°, 120°.$
